Alchemy Approach

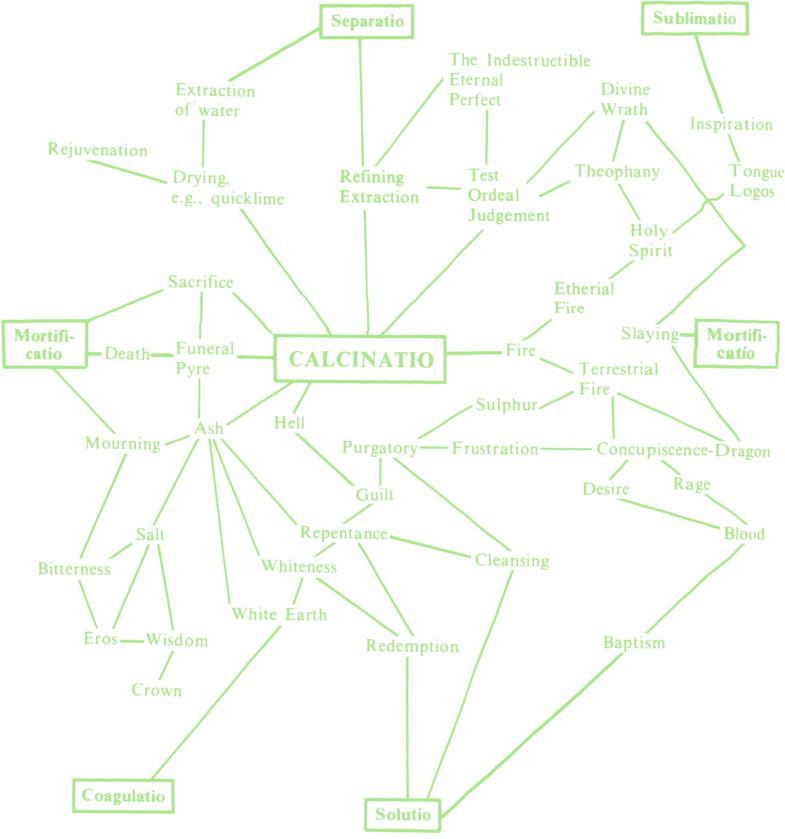
The medieval craft of alchemy sought to transmute base metals into noble ones, most famously lead into gold. The alchemists developed a rich pattern language of operators and transformations

For our purposes here, we want to consider the alchemical processes as analogues to computation. Just as how a working alchemist would apply a sequence of transformations to a material to yield a product, such as rubrification, dissolution, and coagulation, so too can we consider a computational process as a sequence of transformations on data to yield a result.

This is not simply a metaphor! While alchemy as a protoscience was misguided in its goals and methods, the idea that particular operations can be composed to yield results is fundamental to computation. We do not need to adopt the particular operations defined by later alchemists, but find our own.

(Via Leibniz, Wilkins, and others, this tradition did come to distantly influence the development of formal logic and computation theory through Kurt Gödel and friends, but that is a story for another time.)

Generally Computable Functions

Much has been made of “Turing completeness” as the yardstick of a computational system. In general, computer scientists strive to show that a particular system is equivalent in power to a system known to be compatible with Turing machines, such as the lambda calculus or combinatory logic. The Church-Turing thesis posits that any “effectively calculable” function can be computed by a Turing machine, and hence by any Turing-complete system. In other words, to satisfy the threshold of general computability one need meet a certain set of criteria, and then any process can be completed.

So what are the minimum requirements for a system to be Turing complete? It turns out that the requirements are quite minimal (Boolos et al., 2002, “6.2 Minimization”, pp. 70–71). A system need only provide the following operations:

1. A constant function (including zero).

2. An increment (or successor) function.

3. A way to access parameters (or variables).

4. A way to compose functions (or concatenate programs).

5. A way to perform recursion (or looping).

Nock provides all of these building blocks in its primitive opcodes 0-5:

1. Constant (opcode 1)

2. Increment (opcode 4)

3. Parameter selection (opcodes 0 and 9 along with opcodes 7 and 8)

4. Composition (opcodes 7 and 8)

5. Recursion (opcode 0 with, e.g., opcodes 3, 5, and 6)

As you can infer from the compound opcodes, operators can be composed to yield more complex operators.

In this way, we can read a Nock program as a sequence of alchemy-style transformations on data, heightened by Nock’s homoiconicity and self-referentiality.

References

• George S. Boolos, John P. Burgess, and Richard C. Jeffrey. 2002. Computability and Logic. 4th ed. Cambridge: Cambridge University Press.